CNN(二)

2023 iThome 鐵人賽

DAY 19

AI & Data

Fast ai 30天系列第 19 篇

15th鐵人賽

Paul.Ciou

2023-10-04 20:48:27

178 瀏覽

分享至

前一篇講了一些CNN的 kernel, Stride,padding
與如何使用F.conv2d

本章要學習如何建構cnn的learner。

之前第四章有提到基本的神經網路


simple_net = nn.Sequential(
    nn.Linear(28*28,30),
    nn.ReLU(),
    nn.Linear(30,1)
)

那我們把linear 都換成Conv2d 呢?
這樣會無法拿來分類，因為如果這樣寫，會變成一個28x28的觸發圖，
所以我們希望使用stride-2 來縮小，第一次用stride-2 後會變14x14，再用1次會變7x7, 再來4x4 ，2x2 ，最後就會是1x1

所以在這邊先定義一個函式conv 設定他會每次跑完nn.Conv2d 後，就會relu()一次

def conv(ni, nf, ks=3, act=True):
    res = nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)
    if act: res = nn.Sequential(res, nn.ReLU())
    return res

這邊就只是寫個function讓程式較為好看，因為後面要把剛才的28x28 變成1x1

所以現在我們的simple_cnn 就變成下面的

simple_cnn = sequential(
    conv(1 ,4),            #14x14
    conv(4 ,8),            #7x7
    conv(8 ,16),           #4x4
    conv(16,32),           #2x2
    conv(32,2, act=False), #1x1
    Flatten(),
)

Flatten()是一個展平操作，它將多維張量（在這種情況下，是卷積層的輸出）轉換為一維向量。在神經網絡中，通常在卷積層和全連接層之間需要進行這樣的操作，因為全連接層期望輸入是一維向量。

在上述程式中，Flatten()用於將卷積層的輸出從二維空間（例如2x2的特徵圖）轉換為一維向量，以便將其連接到後續的全連接層。這是將卷積神經網絡與全連接神經網絡相連接的關鍵步驟，使得卷積層提取的特徵可以輸入到全連接層進行分類或其他任務。

到這邊我們可以看一下用simple_cnn(xb).shape 來跑第一個mini batch 的型狀會是什麼
可以看到結果是
torch.Size([64,2])
也就是這64張圖片都會被判斷成2個類別。

好了現在可以製做我們的learner了

learn= Learner(dls,simple_cnn,loss_func=F.corss_entropy,metrics=accuracy)

可以用learn.summary() 來觀察Sequential 的狀況

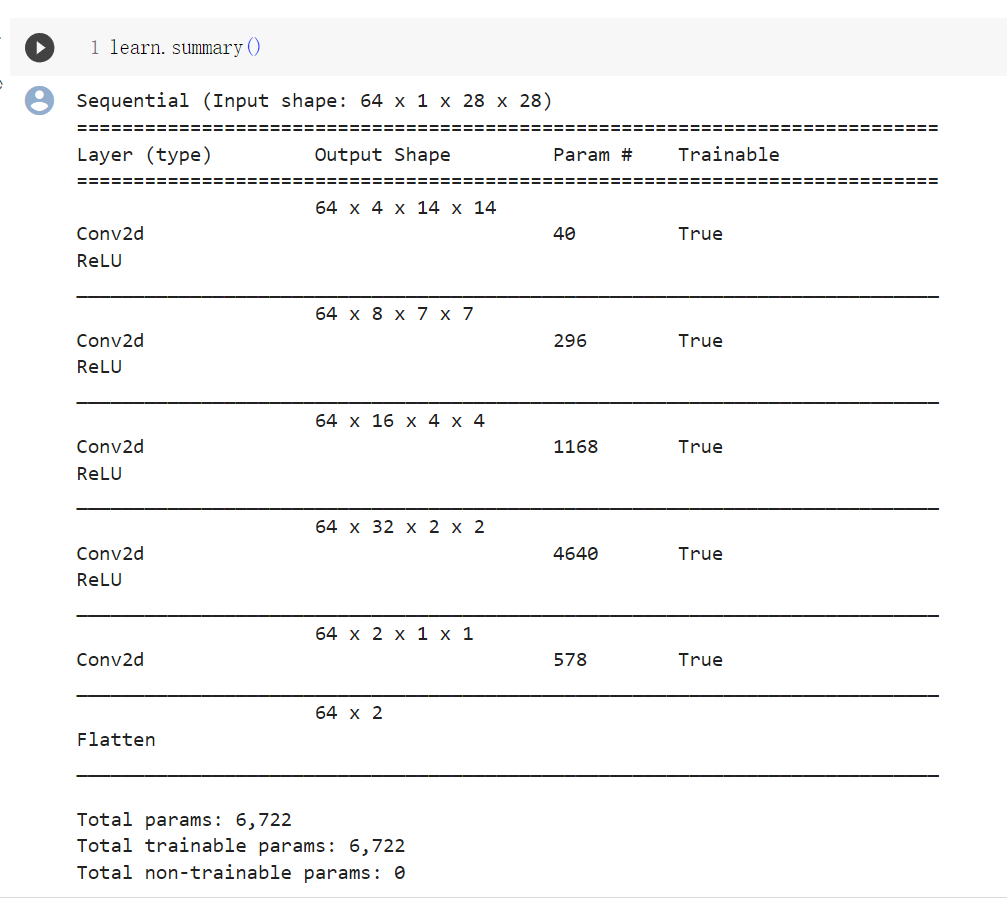
這邊可以看側到最後Conv2d 的輸出是64x2x1x1 ，加入了flatten 後就變成我們要的64x2

接下來我們看一下訓練的結果如何

learn.fit_one_cycle(2,0.001)

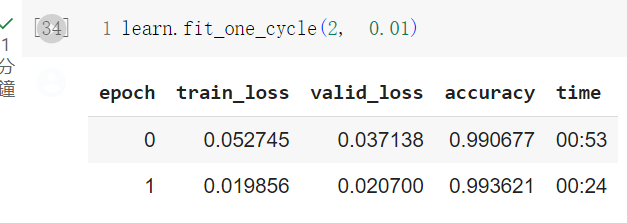
可以看到跑出不錯的結果!

使用全部數據集

之前都只使用3跟7 ，現在要用全部的數據來判別10個類別

一樣先把資料抓進來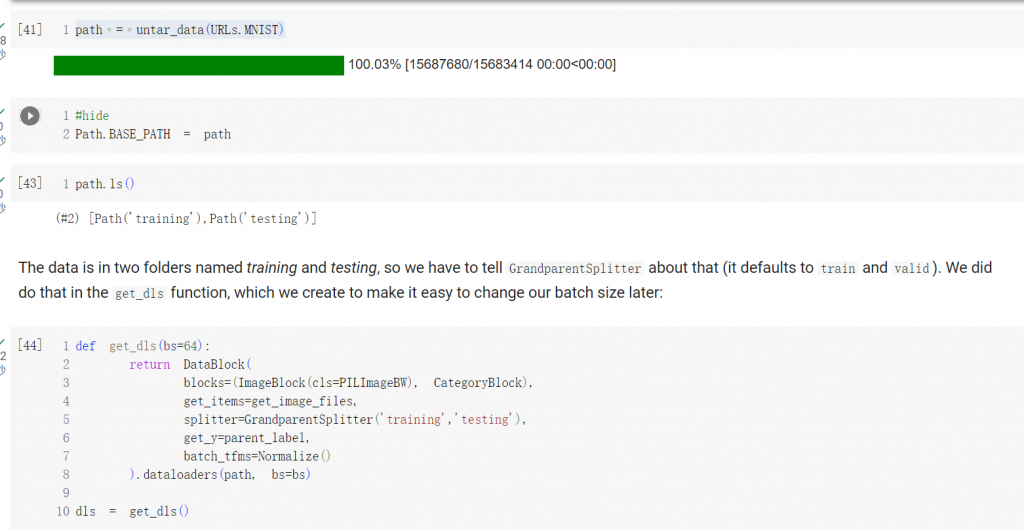

這邊多寫了一個get_dls ，只是方便改變batch size 而已
我們來看一下數據長什麼樣子

準備模型

之前的conv 我們是每一呼叫一次conv2d 就跑一次relu
現在會需要更多觸發，因為有10個類別，同時也應該要更多的kernel

這邊要重複利用之前的conv

def conv(ni, nf, ks=3, act=True):
    res = nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)
    if act: res = nn.Sequential(res, nn.ReLU())
    return res

這邊可以看到stride設成2
通常我們每有一個stride-2 的時候，就會將kernel 的數量加一倍
所以我們每call 一次，kernel 的數量就加倍

在考慮這個之前，我們要計算一下最後的輸出
因為最後我們是希望對應到每一個類別，所以我們會希望feature map 變成1x1
最後再flatten 變成一維向量，最後再經過softmax 後對應到我們的10個類別。

那首先就要來做cnn , 在做cnn 時，因為我們定義的conv 默認stride=2 ，所以我們每做一次大約會縮小1/2 的feature map

照此定義之下，我們的simple_cnn會變成：

def simple_cnn():
    return sequential(
        conv(1 ,8, ks=5),        #14x14
        conv(8 ,16),             #7x7
        conv(16,32),             #4x4
        conv(32,64),             #2x2
        conv(64,10, act=False),  #1x1
        Flatten(),
    )

這邊說明一下為什麼第一層的ks 要設成5，通常在第一層的時候會設定較大的感知區域，另一方面也是講師故意的。
為了讓我們在這邊注意到一件事，就是說如果通道是1，而kerner size 是3x3 , 這樣設定8個kernel 的話，就會
變成9個像素計算8個數字，這樣可能會變成「學不到什麼東西」

所以在這邊如果將kernel 大小設定成5 , 就可以改善這個問題。這邊提出來給讓我們知道一下這個小細節，以免我們犯下這樣的錯誤

設定好squential 就要開始跑我們的leaner 了

def fit(epochs=1):
    learn = Learner(dls, simple_cnn(), loss_func=F.cross_entropy,
                    metrics=accuracy, cbs=ActivationStats(with_hist=True))
    learn.fit(epochs, 0.06)
    return learn
 
learn = fit()

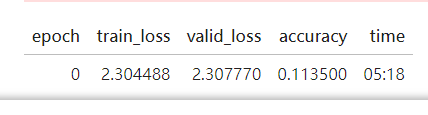
可以看到效果非常差! 跟隨機一樣，因為10類的隨機猜中率也是10%。

那我們該怎麼找出問題呢?

callback

這邊講師就教我們一個很好用的功能：callback

from fastai.callback.hook import *
learn.activation_stats.plot_layer_stats(0)

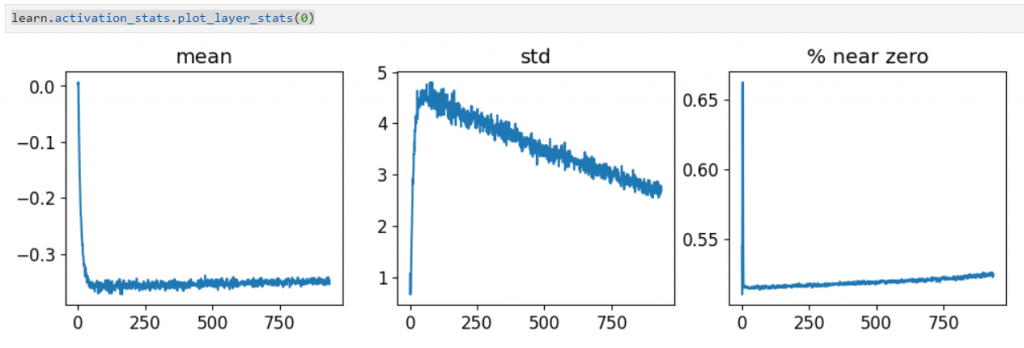
可以看出，在第一層的時候，他的觸發的平均值跟標準差的變化不一致，也相對不平穩，
在接近0的那張圖時最有問題，因為他表示在第一層大部份神經元沒有被激活，這樣到下一層也不會被激活，所以我們可以觀察一下倒數第二層的圖長什麼樣子

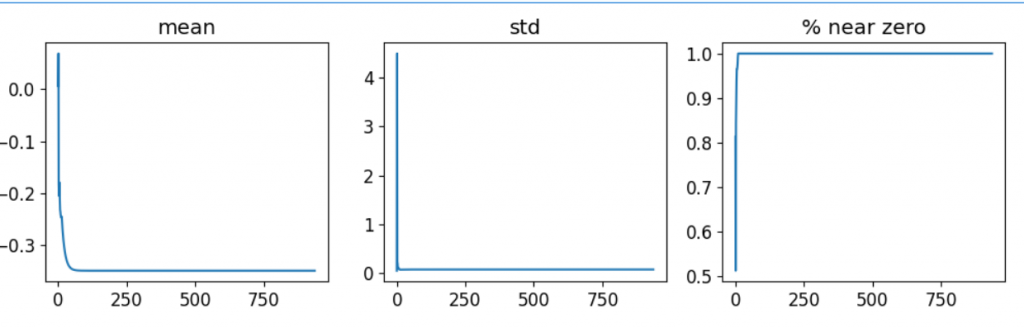
可以看到果然不好

有什麼方法可以改善呢?

增加batch size

本來是64 的我們加到512 試試

dls = get_dls(512)
learn = fit()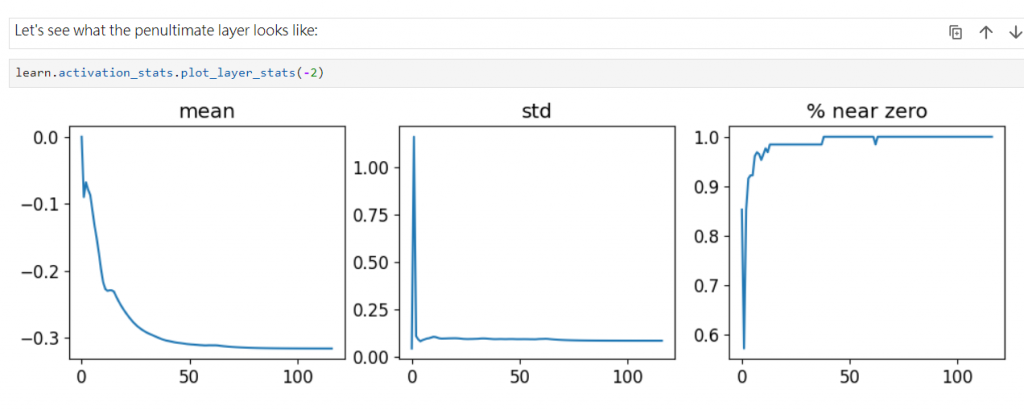

可以看到好像效果還是很差

這邊我們可以拿之前學過的 1cycle training 來試試看

這是一個尋找學習率的工具
重新定義一下我們的fit

def fit(epochs=1, lr=0.06):
    learn = Learner(dls, simple_cnn(), loss_func=F.cross_entropy,
                    metrics=accuracy, cbs=ActivationStats(with_hist=True))
    learn.fit_one_cycle(epochs, lr)
    return learn

其實在分辨3跟7的時候就有用過了

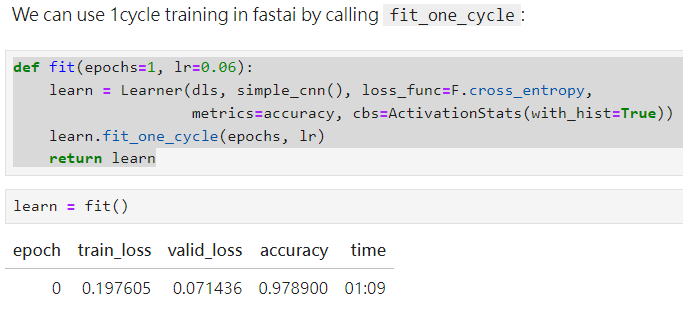
可以看到果然好很多!

所以問題出在學習率嗎，這邊講師也介紹了一些工具來讓我們觀察學習率是怎麼跑的
learn.recorder.plot_sched()

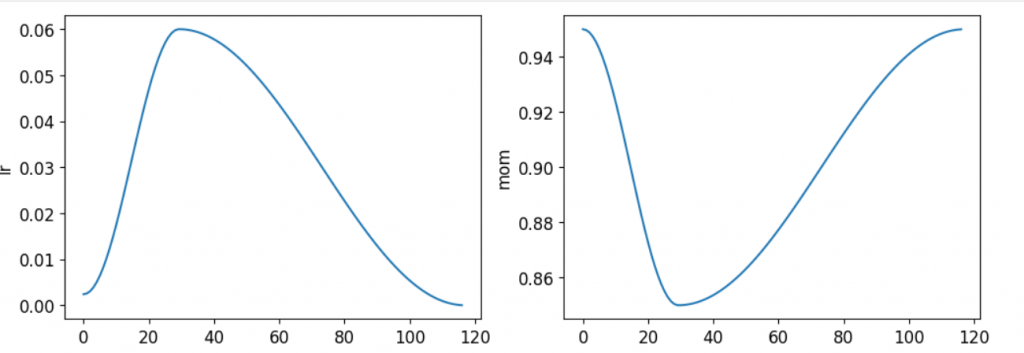
可以看到學習率先上再下，而且很平滑(論文是直上上下)，而他動量變化也很好。

這樣就結束了嗎?
當然沒有，這邊另外介紹了一個工具，讓我們能更好的發現問題與改善他

一樣是觀察剛才的激活狀態，但這邊用了一個可以顯示累積顏色的function

learn.activation_stats.color_dim(-2)

可以看到圖沒有很有，一開始上上又下下的，直到後面才變好
好的情况是訓練一開始就保持平穩，而不是這樣指數級的增長與極度衰減的循環。因為這種循環會導致許多接近0的激活值，這樣會讓訓練變慢而且結果不佳。
那這邊怎麼改善呢?

講師說可以試試Batch Normalization，這是一種用於穩定訓練的技巧，有助於激避免激活值的指數級成長與衰減。

所以重新定義我們的conv2d

def conv(ni, nf, ks=3, act=True):
    layers = [nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)]
    if act: layers.append(nn.ReLU())
    layers.append(nn.BatchNorm2d(nf))
    return nn.Sequential(*layers)

我們加入了 layers.append(nn.BatchNorm2d(nf))

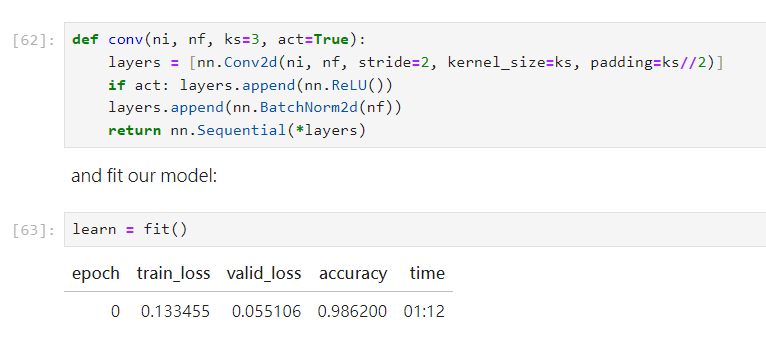
果然改善了一些!

我們再次查看激活狀態

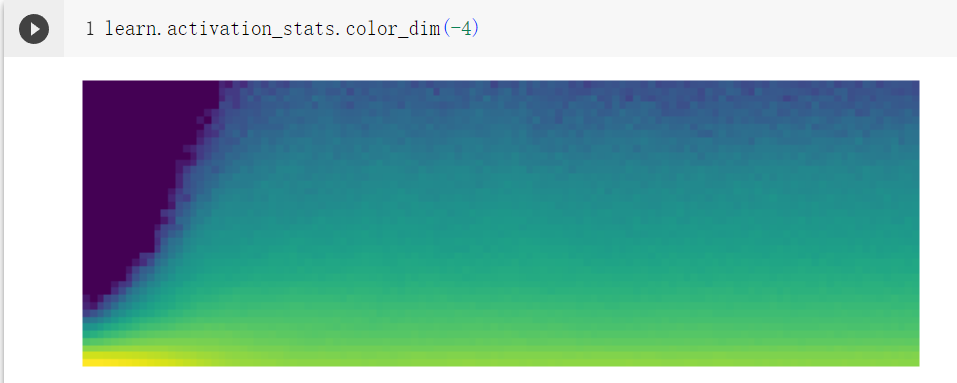
果然平滑了很多
所以跑完就可以得到我們的最終結果

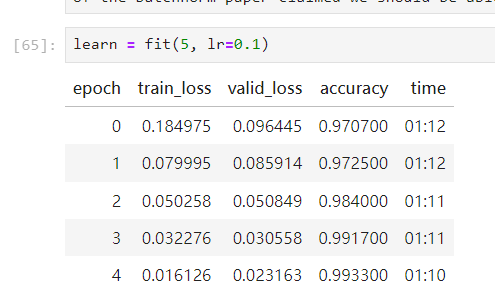
這邊就很好奇，Batch Normalization 怎麼這麼神呢?
作者就花了一些篇幅來講述。歸納如下：
工作原理：

Batch Normalization的主要目標是規範每一層的激活值，以保持它們的均值和標準差在訓練過程中穩定。這是通過計算每一層激活值的均值和標準差來實現的。然後，這些均值和標準差被用來歸一化激活值，使其具有特定的均值和標準差。

不過使用固定的均值和標準差可能會限制模型的表達能力，因為有些激活值可能需要具有較高的值才能進行準確的預測。為了解決這個問題，批歸一化引入了兩個可學習參數，通常稱為gamma和beta。

在進行Batch Normalization後，新的激活值向量y被計算出來。但Batch Normalization層返回的值是
gamma * y + beta。也就是說我們可以通過學習gamma和beta的值來調整激活值，而允許網絡在每一層中學習適合的均值和標準差。

不同階段的行為：

Batch Normalization在訓練和驗證階段的行為不同。在訓練階段，我們使用當前小批次的均值和標準差來歸一化數據，這有助於穩定訓練過程。而在驗證階段，我們使用在訓練過程中計算的均值和標準差的滑動平均值來歸一化數據，這有助於保持一致性並提高模型的泛化性能。

所以說Batch Normalization可以通過歸一化每一層的激活值，並引入可學習參數gamma和beta，使得模型在訓練過程中能夠更好地適應不同的數據分布，從而加速訓練並提高模型性能。

關於Batch Normalization的好處：

Batch Normalization已經在神經網絡中實現了它的承諾，即使的激活值發展平穩，沒有出現“崩潰”現象。這意味著Batch Normalization成功地穩定了訓練過程，使其更加可靠。

含有Batch Normalization層的模型通常比不含有的模型更容易泛化。雖然還沒有對此進行嚴格的分析，但大多數研究人員認為，這是因為Batch Normalization為訓練過程添加了一些額外的隨機性。每個小批次的均值和標準差都會與其他小批次略有不同，因此激活值每次都會被不同的值歸一化。為了進行準確的預測，模型必須學會對這些變化變得更加穩健。通常情況下，為訓練過程添加額外的隨機性通常會有所幫助。

Batch Normalization在現代神經網絡中被廣泛使用，幾乎所有的現代網絡都包含Batch Normalization層或類似的方法。

作者計劃繼續訓練模型，並考慮增加學習率，因為Batch Normalization論文的摘要聲稱我們應該能夠“以更高的學習率訓練”。這表明批歸一化可以允許使用更大的學習率，從而進一步加速訓練過程。

這也就是我們為什麼將lr從0.06 改成0.1 的原因。